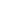Prestressed Concrete Beam Example to British Standards
Prestressed Concrete Beam Design to BS 5400 Part 4
Problem:
Design a simply supported prestressed concrete Y beam which carries a 150mm thick concrete slab and 100mm of surfacing, together with a nominal live load udl of 10.0 kN/m2 and kel of 33kN/m . The span of the beam is 24.0m centre to centre of bearings and the beams are spaced at 1.0m intervals.
γconc. = 24kN/m3
25 units of HB to be considered at SLS for load combination 1 only (BS 5400 Pt4 Cl. 4.2.2)
Loading per beam (at 1.0m c/c)
Note: The loading has been simplified to demonstrate the method of designing the beam (See BS 5400 Pt2, or DB 37/01 for full design loading)
Nominal Dead Loads :
slab = 24 × 0.15 × 1.0 = 3.6 kN/m
beam = say Y5 beam = 10.78 kN/m
surfacing = 24 × 0.1 × 1.0 = 2.4 kN/m
Nominal Live Load :
HA = 10 × 1.0 + 33.0 = 10 kN/m + 33kN
25 units HB = 25 × 10 / 4 per wheel = 62.5 kN per wheel
Load factors for serviceability and ultimate limit state from BS 5400 Part 2 Table 1:
SLS
ULS
Comb 1
Comb 3
Comb 1
Comb 3
Dead Load
γfL concrete
1.0
1.0
1.15
1.15
Superimposed Dead Load
γfL surfacing
1.2
1.2
1.75
1.75
Live Load
γfL HA
1.2
1.0
1.5
1.25
γfL HB
1.1
—
—
—
Temperature Difference
γfL
—
0.8
—
1.0#
Concrete Grades
Beam C40/50 fcu = 50 N/mm2, fci = 40 N/mm2
Slab C32/40 fcu = 40 N/mm2
BS 5400 Pt. 4
Section Properties
cl.7.4.1
Modular ratio effect for different concrete strengths between beam and slab may be ignored.
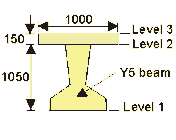
Section properties of Y5 beam were obtained from a Paper by Taylor, Clark and Banks (download .pdf extract from paper by
clicking here).
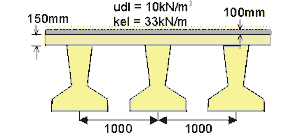
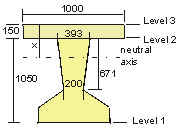
Note: Level 2 is at the nib level and not at the top of the beam.
Property
Beam Section
Composite Section
Area(mm2)
449.22×103
599.22×103
Centroid(mm)
456
623
2nd Moment of Area(mm4)
52.905×109
103.515×109
Modulus @ Level 1(mm3)
116.020×106
166.156×106
Modulus @ Level 2(mm3)
89.066×106
242.424×106
Modulus @ Level 3(mm3)
—
179.402×106
Temperature Difference Effects
Apply temperature differences given in BS 5400 Pt2 Fig.9 (Group 4)to a simplified beam section.
Cl. 5.4.6 - Coefficient of thermal expansion = 12 × 10-6 per °C.
From BS 5400 Pt4 Table 3 : Ec = 34 kN/mm2 for fcu = 50N/mm2
Hence restrained temperature stresses per °C = 34 × 103 × 12 × 10-6 = 0.408 N/mm2
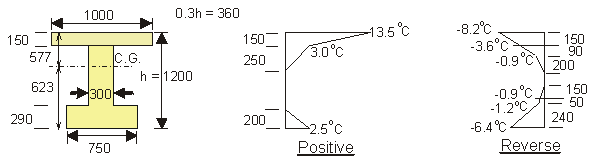
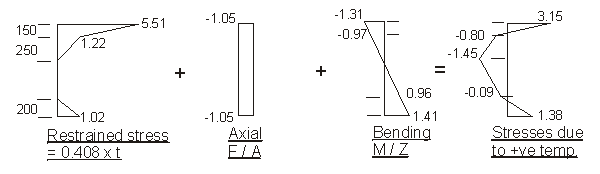
a) Positive temperature difference
Force F to restrain temperature strain :
0.408 × 1000 × [ 150 × ( 3.0 + 5.25 ) ] × 10-3 +
0.408 × ( 300 × 250 × 1.5 + 750 × 200 × 1.25 ) × 10-3 =
504.9 + 122.4 = 627.3 kN
Moment M about centroid of section to restrain
curvature due to temperature strain :
0.408 × 1000 × [ 150 × ( 3.0 × 502 + 5.25 × 527 ) ] × 10-6 +
0.408 × ( 300 × 250 × 1.5 × 344 - 750 × 200 × 1.25 × 556 ) × 10-6
= 261.5 - 26.7 = 234.8 kNm
b) Reverse temperature difference
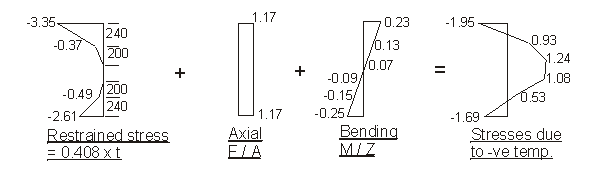
Force F to restrain temperature strain :
- 0.408 × [ 1000 × 150 × ( 3.6 + 2.3 ) + 300 × 90 × ( 0.9 + 1.35 )
] × 10-3
- 0.408 × 300 × ( 200 × 0.45 + 150 × 0.45 ) × 10-3
- 0.408 × 750 × [ 50 × ( 0.9 + 0.15 ) + 240 × ( 1.2 + 2.6 ) ] × 10-3
= - 385.9 - 19.3 - 295.1 = - 700.3 kN
Moment M about centroid of section to restrain
curvature due to temperature strain :
- 0.408 × [ 150000 × ( 3.6 × 502 + 2.3 × 527 ) + 27000 × ( 0.9 ×
382 + 1.35 × 397 ) ] × 10-6
- 0.408 × 300 × ( 200 × 0.45 × 270 - 150 × 0.45 × 283 ) × 10-6
+ 0.408 × 750 × [ 50 × ( 0.9 × 358 + 0.15 × 366 ) + 240 × ( 1.2 ×
503 + 2.6 × 543 ) ] × 10-6
= - 194.5 - 0.6 + 153.8 = - 41.3 kNm
BS 5400 Pt.4 cl.7.4.3.4
Use cl.6.7.2.4 Table 29 :
Total shrinkage of insitu concrete = 300 × 10-6
Assume that 2/3 of the total shrinkage of the precast concrete takes
place before the deck slab is cast and that the residual shrinkage
is 100 × 10-6 ,
hence the differential shrinkage is 200 × 10-6
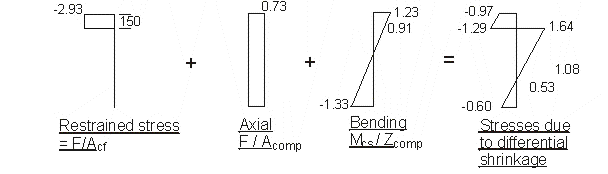
BS 5400 Pt.4 cl.7.4.3.5
Force to restrain differential shrinkage : F = - εdiff
× Ecf × Acf × φ
F = -200 × 10-6 × 34 × 1000 × 150 × 0.43 = -439 kN
Eccentricity acent = 502mm
Restraint moment Mcs = -439 × 0.502 = -220.4 kNm
Self weight of beam and weight of deck slab is supported by the beam. When the deck slab concrete has cured then any further loading (superimposed and live loads) is supported by the composite section of the beam and slab.
Dead Loading (beam and slab)
Total load for serviceability limit state = (1.0 × 3.6)+(1.0 × 10.78) = 14.4kN/m
Design serviceability moment = 14.4 × 242 / 8 = 1037 kNm
Combination 1 Loading
Super. & HA live load for SLS:
= [(1.2 × 2.4)+(1.2 × 10)]udl & [(1.2 × 33)]kel
= (2.88 + 12.0)udl & 39.6kel
= 14.9 kN/m & 39.6kN
Super. & HB live load for SLS:
= 2.88 & 4 wheels @ 1.1 × 62.5
= 2.9 kN/m & 4 wheels @ 68.75 kN
Total load for ultimate limit state:
= [(1.15 × 3.6)+(1.15 × 10.78)+(1.75 × 2.4)+(1.5 × 10)]udl & [(1.5 × 33)]kel
= (4.14 + 12.40 + 4.20 + 15.0)udl & 49.5kel
= 35.7 kN/m & 49.5kN
HA Design serviceability moment:
= 14.9 × 24.02 / 8 + 39.6 × 24 / 4
= 1310 kNm
25 units HB Design SLS moment:
= 2.9 × 24.02 / 8 + 982.3(from grillage analysis)
= 1191.1 kNm
Design ultimate moment:
= 35.7 × 24.02 / 8 + 49.5 × 24 / 4
= 2867 kNm
Combination 3 Loading
Super. & HA live load for SLS:
= [(1.2 × 2.4)+(1.0 × 10)]udl & [(1.0 × 33)]kel
= (2.88 + 10.0)udl & 33kel
= 12.9 kN/m & 33kN
Total load for ultimate limit state:
= [(1.15 × 3.6)+(1.15 × 10.78)+(1.75 × 2.4)+(1.25 × 10)]udl & [(1.25 × 33)]kel
= (4.14 + 12.40 + 4.20 + 12.5)udl & 41.3kel
= 33.2 kN/m & 41.3kN
Design serviceability moment:
= 12.9 × 24.02 / 8 + 33 × 24 / 4
= 1127 kNm
Allowable stresses in precast concrete
At transfer :
cl.6.3.2.2 b)
Compression ( Table 23 )
0.5fci (≤ 0.4fcu) = 20 N/mm2 max.
cl.6.3.2.4 b)
Tension = 1.0 N/mm2
At serviceability limit state :
cl.7.4.3.2
Compression (1.25 × Table 22)
1.25 × 0.4fcu = 25 N/mm2
Tension = 0 N/mm2 (class 1) & 3.2 N/mm2 (class 2 - Table 24)

Stresses at Level 1 due to SLS loads (N/mm2) :
Comb 1
(HA)
Comb 1
(HB)
Comb 3
Dead Load M / Z = (1037 × 106) / (116.020 × 106)
-8.94
-8.94
-8.94
Super. & Live Load M / Z = M / (166.156 × 106)
-7.88
-7.17
-6.78
Reverse Temperature = γfL × -1.69 = 0.8 × -1.69
—
—
-1.35
Differential shrinkage
-0.60
-0.60
-0.60
Total Stress at Level 1 =
-17.42
-16.71
-17.67*
Hence Combination 3 is critical
Prestressing Force and Eccentricity
Using
straight, fully bonded tendons (constant force and eccentricity).
Allow for 20% loss of prestress after transfer.
Initial prestress at Level 1 to satisfy class 2 requirement for SLS
(Comb. 3).
Stress at transfer = ( 17.67 - 3.2 ) / 0.8 = 18.1 N/mm2 (use allowable stress of 20 N/mm2)
The critical section at transfer occurs at the end of the transmission zone. The moment due to the self weight at this section is near zero and initial stress conditions are:
P/A + Pe/Zlevel 1 = 20 ..................... (eqn. 1)
P/A - Pe/Zlevel 2 >= - 1.0 ..................... (eqn. 2)
(eqn. 1) × Zlevel 1 + (eqn. 2) × Zlevel 2 gives :
P >= A × (20 × Zlevel 1 - 1.0 × Zlevel 2) / (Zlevel 1 + Zlevel 2)
P = 449.22 × 103 × ( 20 × 116.02 - 89.066) / ( 116.02 + 89.066) × 10-3 = 4888 kN
Allow 10% for loss of force before and during transfer,
then the initial force Po = 4888 / 0.9 = 5431kN
Using 15.2mm class 2 relaxation standard strand at maximum initial force of 174kN (0.75 × Pu)
Area of tendon = 139mm2
Nominal tensile strength = fpu =1670 N/mm2
Hence 32 tendons required.
Initial force Po = 32 × 174 = 5568 kN
P = 0.9 × 5568 = 5011 kN
Substituting P = 5011 kN in (eqn. 2)
e <= Zlevel 2 / A + Zlevel 2 / P = (89.066 × 106 / 449.22 × 103) + (89.066 × 106 / 5011 × 103)
e = 198 + 18 = 216 mm
Arrange 32 tendons symmetrically about the Y-Y axis to achieve an eccentricity of about 216mm.
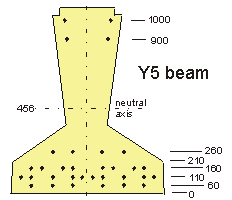
Taking moments about bottom of beam :
2 @
1000 =
2000
2 @
900 =
1800
4 @
260 =
1040
8 @
160 =
1280
10 @
110 =
1100
6 @
60 =
360
32
7580
e = 456 - 7580 / 32 = 456 - 237 = 219mm
Allowing for 1% relaxation loss in steel before transfer and elastic deformation of concrete at transfer :
cl. 6.7.2.3
P = 0.99 Po / [ 1 + Es × (Aps / A) × (1 + A × e2 / I) / Eci ]
P = 0.99 × Po / [ 1 + 196 × ( 32 × 139 / 449220) × (1 + 449220 × 2192 / 52.905 × 109) / 31 ]
P = 0.91 Po = 0.91 × 5568 = 5067 kN
Initial stresses due to prestress at end of transmission zone :
Level 1 : P / A × ( 1 + A × e / Zlevel 1 ) = 11.3 × ( 1 + 219 / 258 ) = 20.89 N/mm2
(20.89 N/mm2 is slightly greater than the allowable of 20 N/mm2 so a number of tendons will need to be debonded near the ends of the beam).
Level 2 : P / A × ( 1 - A × e / Zlevel 2 ) = 11.3 × ( 1 - 219 / 198 ) = - 1.20 N/mm2
Moment due to self weight of beam at mid span = 10.78 × 242 / 8 = 776.2 kNm
Stress due to self weight of beam at mid span :
@ Level 1 = - 776.2 / 116.02 = - 6.69 N/mm2
@ Level 2 = 776.2 / 89.066 = 8.71 N/mm2
Initial stresses at mid span :
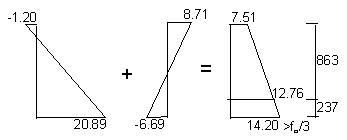
cl. 6.7.2.5
Allowing for 2% relaxation loss in steel after transfer,
concrete shrinkage εcs = 300 × 10-6
and concrete specific creep ct = 1.03 × 48 × 10-6 per N/mm2
Loss of force after transfer due to :
cl. 6.7.2.2
Steel relaxation = 0.02 × 5568 = 111
cl. 6.7.2.4
Concrete shrinkage = (εcs × Es × Aps ) = 300 × 10-6 × 196 × 32 × 139 = 262
cl. 6.7.2.5
Concrete creep = ( ct × fco × Es × Aps ) = 1.03 × 48 × 10-6 × 12.76 × 196 × 32 × 139 = 550
Total Loss = 111 + 262 + 550 = 923 kN
Final force after all loss of prestress = Pe = 5067 - 923 = 4144 kN (Pe/P = 0.82)
Final stresses due to prestress after all loss of prestress at :
Level 1 f1,0.82P = 0.82 × 20.89 = 17.08 N/mm2
Level 2 f2,0.82P = 0.82 × - 1.20 = - 0.98 N/mm2
Combined stresses in final condition for worst effects of design loads, differential shrinkage and temperature difference :
Level 1, combination 1 HB : f = 17.08 - 16.71 = 0.37 N/mm2 (> 0 hence O.K.)
Level 1, combination 3 : f = 17.08 - 17.67 = - 0.59 N/mm2 (> - 3.2 hence O.K.)
Level 2, combination 1 : f = - 0.98 + 1037 / 89.066 + 1310 / 242.424 + 1.64 = 17.71 (< 25 O.K.)
Level 3. combination 3 : f = (1127 / 179.402) + (0.8 × 3.15) = 8.8 N/mm2 (< 25 O.K.)
Ultimate Capacity of Beam and Deck Slab
(Composite Section)
Ultimate Design Moment = γf3 × M = 1.1 × 2867 = 3154 kNm
cl. 6.3.3
Only
steel in the tension zone is to be considered :
Centroid of tendons in tension zone = (6×60 + 10×110 + 8×160 +
4×260) / 28 = 135mm
Effective depth from Level 3 = 1200 - 135 = 1065mm
Assume that the
maximum design stress is developed in the tendons, then :
Tensile force in tendons Fp = 0.87 × 28 × 139 × 1670 × 10-3 = 5655
kN
Compressive
force in concrete flange :
Ff = 0.4 × 40 × 1000 × 150 × 10-3 = 2400 kN
Let X = depth to neutral axis.
Compressive force in concrete web :
Fw = 0.4 × 50 × [393 - (393 - 200) × (X - 150) / (671 ×
2)] × (X - 150) × 10-3
Fw = ( -2.876X2 + 8722.84X - 1243717) × 10-3
Equating forces to obtain X :
5655 = 2400 + ( -2.876×2 + 8722.84X - 1243717) × 10-3
X = 659 mm
Stress in tendon
after losses = fpe = 4144 × 103 / (32 × 139) =
932 N/mm2
Prestrain εpe = fpe
/ Es = 932 / 200 × 103 = 0.0047
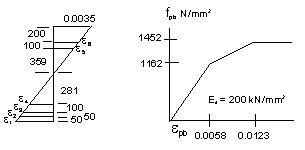
Determine depth to
neutral axis by an iterative strain compatibility analysis
Try X = 659 mm as an initial estimate
Width of web at this depth = 247mm
εpb6 = ε6 + εpe = -459 × 0.0035 / 659 + 0.0047 = 0.0022
εpb5 = ε5 + εpe = -359 * 0.0035 / 659 + 0.0047 = 0.0028
εpb4 = ε4 + εpe = 281 * 0.0035 / 659 + 0.0047 = 0.0062
εpb3 = ε3 + εpe = 381 * 0.0035 / 659 + 0.0047 = 0.0067
εpb2 = ε2 + εpe = 431 * 0.0035 / 659 + 0.0047 = 0.0069
εpb1 = ε1 + εpe = 481 * 0.0035 / 659 + 0.0047 = 0.0072
fpb6 = 0.0022 × 200 × 103 = 444 N/mm2
fpb5 = 0.0028 × 200 × 103 = 551 N/mm2
fpb4 = 1162 + 290 × (0.0062 - 0.0058) / 0.0065 = 1178 N/mm2
fpb3 = 1162 + 290 × (0.0067 - 0.0058) / 0.0065 = 1201 N/mm2
fpb2 = 1162 + 290 × (0.0069 - 0.0058) / 0.0065 = 1213 N/mm2
fpb1 = 1162 + 290 × (0.0072 - 0.0058) / 0.0065 = 1225 N/mm2
Tensile force in tendons :
Fp6 = 2 × 139 × 444 × 10-3
= 124
Fp5 = 2 × 139 × 551 × 10-3
= 153
Fp4 = 4 × 139 × 1178 × 10-3
= 655
Fp3 = 8 × 139 × 1201 × 10-3
= 1336
Fp2 = 10 × 139 × 1213 × 10-3
= 1686
Fp1 = 6 × 139 × 1225 × 10-3
= 1022
Ft = ∑ Fp1 to 6 = 4976 kN
Compressive force in concrete :
Ff = 0.4 × 40 × 1000 × 150 × 10-3 = 2400
Fw = 0.4 × 50 × 0.5 × (393 + 247) × (659 - 150) × 10-3 = 3258
Fc = Ff + Fw = 5658 kN
Fc > Ft therefore reduce depth to neutral axis and repeat the calculations.
Using a depth of 565mm will achieve equilibrium.
The following forces are obtained :
Fp6 = 134
Ff = 2400
Fp5 = 168
Fw = 2765
Fp4 = 675
Fc = 5165
Fp3 = 1382
Fp2 = 1746
Fp1 = 1060
Ft = 5165
Taking Moments about the neutral axis :
MFp6 = 134 × -0.365 =
-49
MFp5 = 168 × -0.265 =
-45
MFp4 = 675 × 0.375 =
253
MFp3 = 1382 × 0.475 =
656
MFp2 = 1746 × 0.525 =
917
MFp1 = 1060 × 0.575 =
610
MFf = 2400 × 0.49 =
1176
MFw = 3258 × 0.207 =
674
Mu = ∑ MFp1 to 6 + MFf + MFw = 4192 kNm > 3154 kNm hence O.K.
cl. 6.3.3.1
Mu / M = 4192 / 3154 = 1.33 ( > 1.15 ) hence strain in outermost tendon O.K.
cl. 6.3.4
The Shear Resistance of the beam needs to be determined in accordance with clause 6.3.4. and compared with the ultimate shear load at critical sections.
Contact David Childs